Em matemática , o conceito de derivada é usado para descrever a inclinação do gráfico de uma dada função, para um dado valor de x. Também pode ser interpretada como o quanto y varia em função de x.

Use a definição de derivada para calcular a derivada f ' (x), para :


















Exemplo 5






Resumidamente : A derivada de uma função f(x) pode ser definida como sendo outra função f '(x) [lê-se f linha] onde :

Exemplo 1
Use a definição de derivada para calcular a derivada f ' (x), para :

Solução
O primeiro passo é calcular f (x+h) para isto, temos que substituir cada x que está na função por x+h

Desenvolvendo ...

Já que podemos notar que f(x) é a função dada no exercício , temos que substituir o f(x+h) -f(x) , na fórmula :

Continuando...podemos eliminar o x^2 com o -x^2 e o +1 com o - 1 porque a soma deles dá zero

Agora vamos colocar o h em evidência e depois substituir o h tendendo a 0

Exemplo 2

a) derivada f ' (x)
b) f ' (4)
b) f ' (4)
Solução a)
O primeiro passo é calcular f (x+h) para isto, temos que substituir cada x que está na função por x+h

Agora vamos desenvolver a função

Continuando ..

Já que podemos notar que f(x) é a função dada no exercício , temos que substituir o f(x+h) -f(x) , na seguinte fórmula :



Substituindo
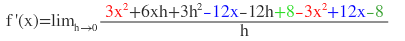
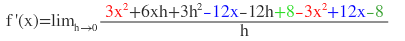
Continuando...podemos eliminar o 3x^2 com o -3x^2 e o +8 com o - 8, bem como o -12x e o +12x porque a soma deles dá zero.

Já que colocamos o h em evidência, teremos :


Solução b)
Levando o valor de x = 4 em f ' (x)= 6x-12 , teremos :
f ' (4) = 6*4 -12 = 12
Exemplo 3
Se y = 3x^2 - 12x + 8 , use o resultado do exemplo 2 para determinar
3.1 - o coeficiente angular da tangente ao gráfico desta equação no ponto p (3, 1).
3.2 - o ponto do gráfico em que a tangente é horizontal .
Solução 3.1
Se f(x)=3x^2 -12x + 8 , o coeficiente angular da tangente em [x , f(x)] será :
f ' (x) = 6x - 12
Para a gente calcular o coeficiente angular da tangente no ponto p(3,1) será:
f '(3)= 6*3 -12 = 6
Obs: podemos notar que o ponto p(3,1) significa que x= 3 e y =1
Solução 3.2
A tangente sempre vai ser horizontal se f '(x) = 0, portanto :
6x-12= 0, obtendo x= 12/6 = 2
Agora vamos substituir o x = 2 em y = 3x^2 - 12x +8 ,ou seja, y= -4
Logo , a tangente é horizontal em Q(2 , -4)
Exemplo 4

Solução
O primeiro passo é calcular f (x+h) para isto, temos que substituir cada x que está na função por x+h

Já que podemos notar que f(x) é a função dada no exercício , temos que substituir o f(x+h) -f(x) , na seguinte fórmula :

Substituindo teremos :

Para a gente conseguir seguir em frente tem que utilizar a técnica de racionalização de frações


Continuando ...

Partindo do principio de que o 2 (expoente) cancela a raiz ,teremos :

Agora podemos dividir o h do numerador pelo h do denominador que vai ser igual a 1

Finalmente

Exemplo 5

Solução
O primeiro passo é calcular f (x+h) para isto, temos que substituir cada x que está na função por x+h


O primeiro passo é calcular f (x+h) para isto, temos que substituir cada x que está na função por x+h

Já que podemos notar que f(x) é a função dada no exercício , temos que substituir o f(x+h) -f(x) , na seguinte fórmula :

Continuando...

Agora vamos desenvolver as funções e simplificar

O exercício está bonitinho , só falta mais um pouco

Continuando...

Finalizando, teremos :

obrigado me ajudou muito a organizar eu sempre erro ao substituir p valor de x mas com a vossa ajuda acabei entendendo tudo
ResponderExcluirOlá! Obrigado pelo feedback, saiba que nosso compromisso é e sempre será, tornar fácil e compreensível um determinado assunto. Take care!
ExcluirSempre será com x tendendo à 0.
ResponderExcluirobrigado
ResponderExcluir