exercícios resolvidos sobre formas indeterminadas de limites

No cálculo de limites de funções , nem sempre ao substituir o valor pelo qual o x está tendendo na função dada, vamos encontrar um resultado definido .

E sempre que temos uma situação não definida , procuramos de algum modo defini-la e para o cálculo de limites ,vamos utilizar a regra de L'Hôpital para que todo exercício em que encontrarmos uma forma indeterminada(resultado indefinido), possamos utilizá-la com o maior prazer e delicadeza para encontrar o resultado .

Em cálculo, uma forma indeterminada é uma expressão algébrica do tipo:

\ Frac {0} {0} \ qquad \ frac {\ infty} {\ infty} \ qquad 0 \ cdot \ infty \ qquad 1 ^ \ infty \ qquad 0 ^ 0 \ qquad \ infty ^ 0 \ qquad + \ infty- \ infty

Obs: Neste artigo ,vamos estudar a primeira e a segunda forma indeterminada de limites que são muito comuns em cálculo.

Se no cálculo do limite de um quociente de funções , tanto o numerador , quanto o denominador tendem a zero , diz-se que tal limite é uma indeterminação do tipo 0/0

Solução : L'Hôpital

Exemplo

Determinar o limite da seguinte função

Solução

Chegamos à uma indeterminação do tipo 0/0 .

Temos que utilizar a regra de L'Hôpital para dar solução.

A Regra de L’ Hôpital diz que o limite de uma função quociente é igual aos limites dos quocientes de suas derivadas, ou seja : vamos diferenciar ou derivar o numerador e o denominador e depois achar o limite .

Atenção: muita gente erra esse tipo de exercício,porque pensa que tem que aplicar a regra do quociente para derivadas e não é isso ...você vai derivar isoladamente cada função.

Depois de diferenciar o numerador e o denominador chegamos à uma outra expressão e , é nesta nova expressão que vamos calcular o nosso lim de x tendendo a 16

Solução : L'Hôpital

Exemplo

Solução

Temos que utilizar a regra de L'Hôpital para dar solução.

Podemos notar que chegamos novamente em uma indeterminação , ou seja, vamos utilizar mais uma vez a regra de L'Hôpital.

ANOTE AÍ

1- Infinito dividido por qualquer número (exceto zero e o próprio infinito) resulta no próprio infinito, respeitando-se também a regra de sinais das operações matemáticas.

O caso em que se tem infinito dividido pelo próprio infinito é chamado de indeterminação.

2- Qualquer número dividido por ∞ (infinito) ou -∞ (menos infinito) irá tender sempre a zero,ou seja,será igual a zero(0).

3- O resultado de uma divisão de um número diferente de 0 por 0 tende ao infinito. Ex: 2/0 ,100/0 etc.

Seção de exercícios

Determine o limite das seguintes funções

Solução

Temos uma indeterminação , aplicar L'Hôpital

Solução

Aplicando L'Hôpital,vem que :

Solução

Aplicando L'Hôpital,vem que :

Solução

Aplicando L'Hôpital,vem que :

Você pode notar que encontramos novamente uma indeterminação .

Então, temos que aplicar novamente a regra de L'Hôpital na última função calculada

Solução

Aplicando L'Hôpital,vem que :

Temos que aplicar novamente a regra de L'Hôpital porque encontramos uma indeterminação

Faça o SIMULADO abaixo e teste seus conhecimentos

SOLUÇÃO : PASSO A PASSO

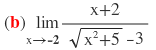
Comentários

Postagens mais visitadas deste blog

Exercícios resolvidos de provas sobre espaço amostral e probabilidade de um evento

Esta lista de exercícios , é resultado de um estudo amplo com o objetivo de descomplicar a análise de espaço amostral e probabilidade de eventos sem utilizar aqueles métodos como Diagrama em árvore e tabela de dupla entrada (produto cartesiano) que muitos professores utilizam para dificultar um pouco o entendimento de probabilidade. Os exercícios estão divididos em 3 seções : Seção de exercícios Básicos ,Seção de exercícios com um certo grau de dificuldade e uma seção sobre prova teste ou simulado. Definições Espaço amostral (S) É o espaço de amostragem de todos os elementos de um experimento probabilístico . Por exemplo: no lançamento de uma moeda,os elementos pertencentes a uma moeda, são : a cara e a coroa, somente é possível obter ou cara ou coroa e o nosso espaço amostral será : S ={ cara, coroa }, um outro exemplo bacana é o lançamento de um dado que pegando o mesmo raciocino , todos os elementos pertencentes a um determinado dado, são os números { 1,2,3,...

Leia mais

Exercícios resolvidos de provas sobre média ,mediana e moda

A média , mediana e moda,são medidas de posição ou medidas de tendencia central que fazem parte de um ramo muito importante da estatística, que é a estatística descritiva . A Estatística Descritiva permite-nos resumir, descrever e compreender os dados de uma distribuição usando medidas de tendência central (média, mediana e moda) e medidas de dispersão (valores mínimo e máximo, desvio padrão e variância). Muitas vezes , a média ,ela é um pouco injusta com a gente sabe porquê ? Imagine o seguinte : Estamos em uma festa com duas pessoas(Pedro e Niko ) e só tem 2 bifes . Só que acontece o seguinte : o pedro por ser guloso vai escondido e come os 2 bifes...Em media ,cada um deles comeu um bife porque a média diz-nos que havia um bife para cada pessoa mas não nos diz como é que os bifes foram distribuídos. Esta é uma das razões pelas quais os dados estatísticos que se apresentam em relatórios de investigação terem frequentemente duas ou mais medidas descritivas associadas. Por ...

Leia mais

Tudo sobre integrais definidas e exercícios resolvidos com comentários

Definição A Integral definida é um tipo de integral que tem um valor inicial que denominamos de limite inferior e um valor final que chamamos de limite superior . Resumidamente a integral definida entre a e b é a integral indefinida em b menos a integral indefinida em a . Teorema fundamental do cálculo Muitas vezes , a gente ouve falar do teorema fundamental do cálculo e tem dificuldade de entender, porque nem todo professor tem paciência de explicar todo esse trem , mas vamos nessa ! O teorema fundamental do cálculo é a base das duas operações centrais do cálculo, diferenciação e integração, que são inversas uma da outra . Isto quer dizer que se uma função contínua é primeiramente integrada e depois diferenciada (ou vice-versa), volta-se na função original. Exemplo :Seja f(x)=2x, Calcule a sua integral e derive o resultado para chegar a função original 2x. Sabendo que a constante c é um número , vamos derivar o resultado para chegar no funçã...

Leia mais

Exercícios resolvidos de provas com comentários sobre distribuição binomial

"Em nossas loucas tentativas, renunciamos ao que somos pelo que esperamos ser".William Shakespeare Antes de entrar no assunto principal vamos entender o que é fatorial de um número que tem como simbolo o n! Na matemática, o fatorial de um número natural n, representado por n!, é o produto de todos os inteiros positivos menores ou iguais a n. A notação n! foi introduzida por Christian Kramp em 1808. Exemplo: Calcule o fatorial dos números 0,1,2,3,4 e 5 . Solução 0! = 1 1! = 1 2! = 2.1 = 2 3! = 3.2.1 = 6 4! = 4.3.2.1 = 24 5! = 5.4.3.2.1 = 120. Observação: O zero não entra nesta definição, pois se multiplicarmos todo o produto de n até 1 por zero teremos zero como resultado. O que é uma distribuição binomial? Em estatística, a distribuição binomial é a distribuição de probabilidade do número de sucessos numa sequência de n tentativas. O que devemos saber sobre essa distribuição? Vamos entender as caraterísticas de um experimento binomial Um exper...

Leia mais

Exercícios resolvidos de provas sobre derivadas aplicando as regras de diferenciação

Para calcular a derivada de uma função que seja derivável, em determinado ponto do seu domínio, podemos sempre usar a definição. Mas, dependendo da função, isto pode significar bastante trabalho e pode ser evitado usando regras de diferenciação, evitando assim complicados cálculos de limites. Em que consistem as regras de derivação ? Resumidamente podemos afirmar que se o cálculo de derivadas usando a definição é meio complexo e gasta mais tempo , usando as regras de diferenciação as coisas ficam um pouco mais tranquilas devido a rapidez na execução e obtenção dos resultados. Entretanto, aplicar as regras de derivação consiste em usar estes conhecimentos para, a partir das derivadas de funções mais simples, determinar as derivadas de funções que delas se obtêm por meio das operações. Simbologia A derivada de uma função f, na variável x , é uma função, que representamos por f ' . Regras a seguir : Sejam f e g funções diferenciáveis : Está regra afirma que...

Leia mais

Exercícios resolvidos sobre cálculo de área em integrais Definidas

O teorema de integral definida para o cálculo de área , diz que : Se f e g são funções definidas e contínuas em [a, b] e tais que f (x) ≥ g(x), . Então a área da região A limitada pelos gráficos de f(x) e g(x) e pelas retas x = a e x = b é dada por: Graficamente Seção de exercícios Determine a área limitada pelas curvas Exercício 1 Solução Primeiro ,vamos calcular as raízes (pontos de interseção) igualando as duas funções : Sempre que temos uma situação como essa, devemos colocar o expoente 2 nas duas funções. Agora, vamos ter que entender o gráfico de cada função envolvida Representando graficamente as curvas, teremos : Calculando a área Exercício 2 Solução Vamos calcular as raízes (pontos de interseção) igualando as duas funções : Chegamos numa equação do segundo grau , e vamos utilizar a fórmula de Bhaskara para encontrar as raízes ou pontos de interseção (x 1 e x 2 ). ...

Leia mais

Factosfera

Pesquisar assunto